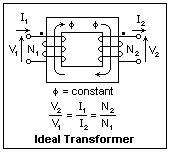
Ideal Transformer

A transformer is a device in which two circuits are coupled by a magnetic field that is linked to both. There is no conductive connection between the circuits, which may be at arbitrary constant potentials. Only changes in one circuit affect the other. The circuits often carry at least approximately sinusoidal currents, and the effect of the transformer is to change the voltages, while transferring power with little loss. Sinusoidal excitation is not necessary, and transformers may handle arbitrary signals, in which the action can be considered as a transformation of impedances. The magnetic field coupling the circuits can be in air, but is usually in a ferromagnetic material, the core, in which the field can be thousands of times greater than it would be in air, making the transformer efficient and small. The transformer is an honorary electrical "machine" in which the flux changes occur by variation in currents with time, instead of by motion.

Most transformers with iron cores can be considered as ideal when you use them. An ideal transformer has no losses, an aim that is closely attained in practice, so the energy transfer from the primary circuit to the secondary circuit is perfect. The diagram represents such a transformer, showing the core with magnetic flux ?, the primary winding of N1 turns, and the secondary winding of N2 turns. The reference directions for the voltages and currents at the terminals are shown. All of these quantities are to be considered as phasor amplitudes, varying sinusoidally with time. Note the dots at one or the other of the terminals of each winding. Currents entering the dotted terminals produce flux in the same direction, the direction shown. The current and voltage ratios are equal to the turns ratio. This means that the power factor (cosine of the phase angle), and the power, are the same at input (primary) and output (secondary). These things you probably already know, and we will not explore their consequences further.

The diagram shows the usual schematic way to represent a transformer. In an actual transformer, the windings are wound on top of each other, not on separate legs, to reduce leakage flux. In the usual shell-type transformer, both primary and secondary are on one leg, and are surrounded by the core. A core-type transformer has windings covering the core legs.

In order to design a transformer, or to examine in more detail how it departs from ideality, it is necessary to understand how a transformer works, not just how to express its terminal relations in an approximate way. It is also important to know how the properties of the iron core affect the performance of the transformer. A real transformer becomes hot because of losses, and the ouput voltage may vary with load even when the primary voltage is held constant.

The mutual flux ? is the means of transfer of energy from primary to secondary, and links both windings. In an ideal transformer, this flux requires negligibly small ampere-turns to produce it, so the net ampere-turns, primary plus secondary, is about zero. When a current is drawn from the secondary in the positive direction, ampere-turns decrease substantially. This must be matched by an equal increase in primary ampere-turns, which is caused by an increase in the current entering the primary in the positive direction. In this way, the back-emf of the primary (the voltage induced in it by the flux ?) equals the voltage applied to the primary, as it must. This fundamental explanation of the operation of a transformer must be clearly understood before proceeding further.

Magnetic Fields

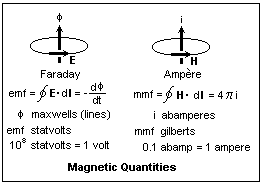
Since magnetic fields play an essential role in transformers, we must review them first. They exert forces on magnetic poles, but here the important thing is that they induce electric fields when they move. A magnetic field is produced surrounding any flow of electric charge, or current. The relation between the magnetic field and the electric current can be most compactly expressed by Ampère's Law, which states that the line integral of the component of the magnetic field along a closed curve is proportional to the current linked by the closed curve. The value of this line integral is called the magnetomotive force, or mmf, around the curve. There are equivalent formulas that give the magnetic field at a point directly in terms of the currents. These also require integration, and are much more difficult to use in the simple cases we require.

The question of units always comes up, and the question is not a pretty one. We'll treat the matter in some detail here, because it is a frequent source of confusion and anguish. If we wish simple formulas, without a lot of constants, we have to massage the units so that it all comes out straight. If we make the choice shown in the box, and measure current in units called absolute amperes, or abamperes, then the magnetic field H comes out in units called oersteds if distance is in centimetres. The value of the mmf can be called so many gilberts if you like, and then oersteds are gilberts per centimeter. The basic concept is current linked per unit length of path, however expressed. We presume that there is some way to define the absolute ampere independently of Ampère's Law.

The unit for current you know is probably ordinary amperes. Then, if we use an even simpler expression for the mmf, omitting the 4?, and use metres for distance, we get a magnetic field in amperes per metre. Here, amperes means the total current. If we have N turns of wire carrying I amperes, we have NI amperes total linking the magnetic field. Hence, people usually speak of ampere-turns in this case. It is the omission of the 4? that makes things confusing, though you can easily work out the relation between ampere-turns/metre and oersted by calculating the field for the same current in the two cases, and comparing the results.

Less weird, perhaps, was the practice in American electrical engineering of using the inch as the length unit. Now we have gilberts per inch for the magnetic field, which is not an oersted, but 1/2.54 of an oersted. One can also speak of ampere-turns per inch in the same way.

Now there is the matter of magnetic flux. Flux is another manifestation of the magnetic field, defined by its ability to induce an electric field when it changes. The basic relation is Faraday's Law. Note the analogy with Ampère's Law. The negative sign (another fertile source of confusion) is there so energy will be conserved, and depends on the positive directions shown in the figure. This requires that if ? is increasing, any current that flows due to the induced voltage must act to decrease ? (Lenz's Law). Check that this is so in the diagram.

The integral of the electric field around a closed curve is called the electromotive force, emf, and is probably a more familiar quantity than the mmf. As in the case of Ampère's Law, we presume that there is some independent way to define an emf, and the unit here is the abvolt. This unit is, in fact, defined by Coulomb's Law, at least in principle. Now, we choose the simplest relation for Faraday's Law, emf = -d?/dt. The unit of flux is such that a change of one unit per second induces an emf of one abvolt. The unit is called a line or a maxwell. Let's use line here, and remember that a magnetic field is not made of physical lines of anything. "Line" is just a conventional name, recalling the representation of a field by lines of force. The flux density B is in lines per square centimetre, units called gauss with G as the symbol.

We now have two quantities, the abampere of current or mmf, and the abvolt of potential or emf, defined in terms of the forces between currents, and between charges, respectively. We also have two definitions of magnetic field, one in terms of mmf per unit length, and the other in terms of emf times seconds. There is really only one magnetic field with two manifestations or properties, though early mechanical theories of electromagnetism considered that one caused the other, like stress caused strain. This interpretation has been fossilized in the Giorgi system of units that is now standard in engineering, and which has caused a great deal of confusion and unnecessary anxiety, especially in magnetism. Things are actually simpler than they have been made out to be.

The big advantage of the definitions of the magnetic field in terms of the abampere and abvolt is that the magnetic field H in oersted comes out to be exactly the magnetic flux density B in gauss. Naturally: they are the same thing, after all. In all the other systems we have skirted around, this is not true. You already know that B = ?0H in Giorgi units. The ?0 is simply a number, not a physical quantity, that adjusts for arbitrary choices of units. It has no physical interpretation whatsoever.

We are rightly very attached to our volt and ampere, the practical units arbitrarly defined by the potential of a Daniell cell and the resistance of a column of mercury early in the history of electromagnetism. Giorgi found that if we took 10 ampere = 1 abampere, and 1 volt = 108 abvolt, approximately, that everything came out wonderfully consistently, so long as the metre was the length unit, not the centimetre. There were some small adjustments in the previous practical units, but this was a small price to pay for having them join an absolute, very scientific, system of units. The opportunity was also taken to remove the factors of 4? from some equations, and add them to other equations, which has complicated things. For any overall view, it is best to consider Maxwell's Equations and the force equations, but what we have done here will do us.

The older way was to use oersted and gauss, with volts and amperes, and inches as the length unit, at least in English-speaking countries. The gauss and oersted have not disappeared, even with Giorgi units everywhere else. In fact, 104 G = 1 Weber, and 1 Tesla = 108 lines. Obviously, 1 T/s = 1 V. If it weren't for the damned 4?, all the new units would differ only by powers of 10 from the old! The Giorgi system is just the old absolute electromagnetic system, tarted up, really. All the fuss over units is actually a blessing; when you understand the units, you will understand electromagnetism.

We all are comfortable with an electric circuit. The current stays in the wires, and the applied emf is equal to the sum of the voltage drops, and the sum of the currents entering a junction is zero. A resistive element has a voltage drop that is proportional to the current. This analogy to friction is actually rather complicated, but at least it looks simple, and all we need is the resistance, R = l / ? A, where ? is the conductivity of the material of uniform cross section A and length l. What happens is that the electric field resulting from the emf causes free electrons to move along the wire. There is an electric field outside the wire as well, but it finds no movable electrons.

An mmf also causes a magnetic field to occur, and it usually just spreads out in space. There are no little free magnetic poles for it to act on, but in iron there are electrons that can be called to attention, so that they all point in roughly the same direction, and hold themselves there by atomic forces. The electrons are spinning charges, and the net effect is that of a lot of small current loops causing a very strong magnetic field. That is, the H field associated with the mmf calls up a total magnetic field in the same direction that we must call B, because it will certainly induce an electric field according to its magnitude. H is only a partial field, produced by whatever makes the mmf, while B is the total field. This is the usual interpretation of H and B, which is quite useful. H and B are not really different kinds of field, except in the imagination. In the Giorgi system, they are expressed in different units, however, which has no physical significance.

So, an mmf is produced by ampere-turns, and in a uniform iron core creates a uniform H field, which snaps the electrons into order making a flux density B ? times larger, and a total flux ? = BA. Just as in the electrical case, there is a magnetic field outside the iron core, but no electrons are there to join the army, so not much flux results. The small flux that does go this way is called leakage flux. Leakage flux is important in transformers. The whole thing is remarkably like a circuit, with mmf in place of emf, and flux in place of current. The analog of resistance is called reluctance, given by the same formula as resistance, but with permeability replacing conductance. The ratio of the permeability in the iron to that in air is about 1000. For electric currents, the ratio of conductivities is a million times greater.

The ideal is to have all the magnetic flux produced by one winding link the other. This is not attained in practical transformers. Flux that does not link both windings is called leakage flux and has the effect of adding an inductance that produces a voltage drop when current is present. Leakage is affected by the shape of the core and by the arrangement of the windings. To reduce leakage, the core must be compact and the windings close together.

Iron

The conductivity of a conductor is practically constant, independent of the current. The permeability of iron is by no means constant. The flux density B of a sample is a nonlinear function of H, given by the magnetization curve. Worse than this, the flux density depends on what has happened in the past, as well as to the current value of H. If H is varied sinusoidally, B follows an S-shaped curve called the hysteresis loop, which is different for every different maximum value of H. B lags behind H in its variation, and energy is lost in a kind of internal friction. The energy lost in each cycle is proportional to the area inside the hysteresis loop. The slope of the approximately linear portions of this loop is the value to be used in estimating the reluctance, which we will discuss later. It is not, incidentally, the slope of the magnetization curve. Refer to books on magnetism for a full discussion of magnetization and hysteresis. There is a lot of lore here.

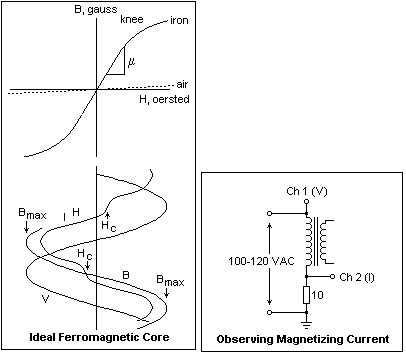
An ideal core material would have a hysteresis loop with no area inside it. In this case, B would be a single-valued function of H, as shown in the diagram on the left. At high values of H, when all the electrons were aligned, the curve would bend over and saturate. Although the iron saturates, the flux continues to increase as in air, so the B curve is never horizontal. It is most economical to operate magnetic materials at as high a flux density as possible, usually near the knee of the curve. Note that the curve in the figure is a hysteresis curve (alternating flux), not a magnetization curve.

In actual magnetic materials, the flux does not drop to zero when the mmf returns to zero, but there is a remanent flux. To reduce the flux to zero, an mmf in the reverse direction called the coercive force must be applied. Now the B vs H curves are moved left and right, without changing their shapes much. The horizontal distance between the curves is twice the coercive force. The ends of the loop depend on the maximum flux density, so there are different hysteresis curves for each maximum flux density. Since the flux lags the current, there is now component of the voltage in phase with the applied current, which means an energy loss, the hysteresis loss. The amount of loss, in ergs per cycle per cubic centimeter, is the area within the hysteresis loop divided by 4?. (Axes are gauss and Oersted.)

If a sinusoidal alternating voltage is applied to the winding creating the emf, the flux is sinusoidal, but the current is not. The current must vary in just such a way as to produce the sinusoidal flux, which is 90° out of phase with the applied voltage. The figure shows a sketch of the current waveform that results. This current, called the magnetization current, will be almost 90° out of phase with the applied voltage, as shown, with a small in-phase component representing hysteresis loss. The magnetizing current shows a strong third harmonic component. The prominent peaking at maximum B is the result of the bending over of the magnetization curve. Note that the flux is a maximum when the voltage is zero, and that the coercive force can be observed in the current waveform, showing that there is a component of the current in phase with the voltage, representing an energy loss. A transformer is designed so that the magnetizing current is a small fraction of the normal load current, usually only a few per cent. Since the flux is accurately sinusoidal, the secondary voltage (and current) will also be sinusoidal. The peculiarities of the magnetizing current will not be reflected in the transformer output, and will not cause distortion.

The magnetizing current can be observed with an oscilloscope using the circuit at the right. The voltage across the 10? current-sensing resistor will be negligible. Channel 1 will be set to 50 V/division, Channel 2 to perhaps 0.2 V/division. If you feed the circuit with a Variac, make QUITE sure that the connection shown grounded is indeed grounded, so it will not conflict with the oscilloscope ground. To be safe, use an isolation transformer. If you know the constructional details of the transformer tested (see the paragraph below on dissecting a transformer), you can find B from the voltage, number of turns and core area, while H can be found from the current, number of turns, and magnetic circuit length. This makes it possible to sketch a hysteresis curve for the transformer core.

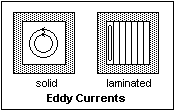As the flux ? varies with time, there will certainly be an induced electric field in the core, and if it is conducting, currents will flow. These are called eddy currents, and are precisely analogous to a short-circuited secondary winding. They will cause heating, and will represent an energy loss. They are minimized by decreasing the conductivity of the iron (silicon iron has a smaller conductivity), and by making the core from a pile of thin laminations insulated from each other. They cannot be reduced to zero, but can be made quite small. Like hysteresis, eddy currents will produce a current in phase with the applied voltage, that is included in the magnetization current. Iron losses, as they are called, are reflected in the in-phase component of the magnetization current.

Ferromagnetic materials saturate at a certain flux, as has been mentioned, and are usually used at fluxes not far below saturation. If the primary of a transformer carries direct current, which is not resisted by inductance but only by the resistance of the winding, which is always low, it is easy to drive the core into saturation for at least part of the cycle. The result is excessive current, first appearing as current spikes, that causes the transformer to heat, and, of course, the transformer action to fail. Transformers must not be subjected to direct currents. This includes secondary windings as well as primary windings, of course.

Some iron-core inductors are designed to carry direct currents. These are chokes that block alternating currents. To prevent saturation, the core is provided with an air gap. Even a small air gap dominates the reluctance and prevents saturation at reasonable currents (the flux is proportional to the ampere-turns). The flux density is kept lower than the saturation value for the iron, of course, but now the inductance is independent of the direct current. In audio transformers for push-pull amplifiers, direct currents flow in the divided primary in opposite directions, so that their mmf's cancel, while the alternating audio signal flows in the whole primary.

Losses and Iron

Early transformers used pure iron for their cores. Pure iron has a hysteresis loss of about 600 ergs per cycle per cubic centimeter, a relatively small value, and a coercive force of 0.2 Oe from 10 kG, so it is magnetically quite "soft." Commercial sheet iron has a larger, but still small, hysteresis loss. However, it is a fairly good electrical conductor, with a resistivity of 7.64 ??-cm. Therefore, it acts like a short-circuited turn, and currents are induced that circle round the magnetic field as it changes. These eddy currents dissipate large amounts of energy, making a solid core very inefficient. This can be overcome by laminating the core, and interrupting the possible current paths. Bundles of wire were used as cores for this purpose, but thin sheet laminations are now the universal practice. The eddy-current loss is proportional to the square of the thickness of the laminations. It's proportional to the squares of the frequency and the maximum flux density as well.

Around 1903, Sir Robert Hadfield discovered that adding silicon to steel greatly increased its resistivity, while affecting the magnetic properties very little. A silicon steel with 4.25% Si has a resistivity of 60 ??-cm. The hysteresis loss is about 1800 ergs per cycle per cubic centimeter, and the coercive force is about 0.4 Oe. The only drawback of silicon is that it makes the steel brittle in such concentrations, making punching and other mechanical operations more difficult. The laminations must be insulated from each other, of course. It seems that originally rust was the insulation, but since rust contributes greatly to hysteresis loss, laminations are now pickled and insulated by a compound. The density of silicon steel is 7.5 g/cc for Si < 2%, and 7.7 g/cc for Si > 2%.

Serendipitously, it was found that steel containing more than 1% Si was not subject to the phenomenon of "ageing" in which the coercive force (and so the hysteresis loss) increased as much as 100% with time, when the iron operated at temperatures above 150 °F (as is often the case) or was subject to mechanical actions. All transformer cores for power frequencies, and parts of rotating machinery subject to alternating fields, are now made of silicon steel, for this and the other reasons mentioned.

With the eddy-current loss problem solved by silicon steel and laminations, the larger part of core loss is hysteresis loss, which is proportional to the frequency (since a fixed amount of energy is lost in each hysteresis cycle). Steinmetz found that the hysteresis loss was W = A B1.6, where B is the maximum flux density. The constant A is about 0.001 for silicon steel, 0.013 for cast iron, and 0.004 for sheet iron. The large value for cast iron should be noted. Magnetic cores for early rotating machines were typically cast iron, which has a relatively high electrical resistance (reducing eddy-current losses) but large hysteresis loss. The eddy-current and hysteresis losses can be separated experimentally by tests at different frequencies, because of their distinct frequency dependences.

Core losses generally determine the power ratings of large transformers, which often must be artificially cooled by forced ventilation or circulating fluids. It is more efficient to design transformers for high maximum flux densities, but this also increases the core losses.

Copper losses are the I2R losses in the windings, and are relatively more important in small transformers than in large. It was the practice to design windings at 700 c.m./A (c.m. = circular mils, the square of the diameter in thousandths of an inch), or alternatively at 500 c.m./A. Many transformers are now designed with as little copper as 340 c.m./A.

Transformer Operation

In a real transformer, we must include the magnetizing current, as well as the effects of leakage flux. Leakage flux links only one winding, and is completely independent of the other. Its effect is to act like an inductance in series with a winding. In addition, there is the IR drop in the copper of a winding when it carries current. These are the things that make a real transformer behave differently from an ideal transformer. If we just talk about these things, we soon are mired in a swamp of phase angles and relative directions that make understanding very difficult. The best way to understand things is to draw a phasor diagram of the currents, voltages and fluxes. In doing this, we draw the diagram in stages, showing how to proceed step by step so that it would be possible to make accurate numerical estimates of each quantity. The magnetizing current is not well-represented by a phasor, since it is nonsinusoidal, but this causes no serious inaccuracy, since most of the quantities in a transformer under load are sinusoidal.

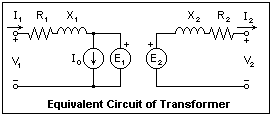
Before a phasor diagram can be drawn, a circuit diagram showing the connections and the positive directions of each circuit quantity is necessary. Such a diagram is shown at the right. It is not really complete, since it does not show the connection through the flux ? that reflects equal induced voltages and currents from secondary to primary. This is hinted at by the generators marked E. When the phasor diagram is drawn, we will reverse the positive directions in the primary to separate the two parts of the diagram so that they will not fall on top of each other. The diagram shows the winding resistances R, and the reactances due to the leakage fluxes X, as well as a current generator for the magnetizing current I0. We will assume that the turns ratio is unity for convenience, so the vectors turn out to be about the same lengths on the same scale. If the turns ratio were not unity, the voltages and currents would be reflected into the primary multiplied by the proper ratios.

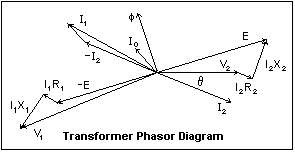
The phasor diagram for the transformer at full load is shown at the left. This complicated diagram can be understood by following through how it was constructed. We start by assuming that the secondary is supplying a current I2 at a terminal voltage V2 with phase angle ?. These are the first two phasors drawn. Now, to V2 we add I2R2 in phase with I2, and I2X2 in quadrature, to find the induced voltage E in the secondary. The voltage -E is induced in the primary. The flux ? is at right angles to E, as shown. The current I0 is necessary to create the flux, and is drawn with its proper relation to ?. The current I2 is reflected to the primary as -I2, and added to I0 to find the total primary current I1. Now that we know I1, we can add I1R1 and I1X1 to -E to find the primary terminal voltage, V1. In this diagram, the magnetizing current, and the voltages due to leakage flux and winding resistance, are greatly magnified so their effects can easily be seen. As an exercise, draw a phasor diagram for an open secondary, when I2 is zero, and find V1 for this case. Also, draw diagrams for various phase angles ?.

Try to visualize what happens when the secondary current decreases. It may help to draw additional phasor diagrams. The difference between the terminal voltage V2 and the induced voltage E becomes less, and they approach one another. The magnetizing current becomes a larger part of the smaller primary current, which changes in phase accordingly. The flux, of course, remains the same. The input voltage decreases, and becomes equal to V2. One of the important characteristics of a transformer is its regulation, the change in output voltage between no load and full load, divided by the full-load output voltage (or some such definition), expressed as a percentage. This is practically the same as the difference between the full-load and no load input voltages divided by the no-load input voltage, holding the output voltage constant, and this latter quantity can be read off the full-load vector diagram. The no-load input voltage is V2, and the full-load input voltage is V1. Typical power transformer regulation is around 1% or even less at unity power factor, falling off to a few percent at 0.8 pf. Such transformers are called constant-potential transformers. Regulation is improved by decreasing leakage flux and winding resistance. If poor regulation is desirable, it can be obtained by increasing the leakage flux without added resistive heating.

The efficiency of a transformer is quite high, usually over 98% at full load. It increases at partial load, sometimes to over 99%. A real transformer is not very far from an ideal transformer, in fact. These figures for efficiency and regulation apply to large power and distribution transformers, say above about 5 kVA capacity (product of rated voltage and current) with silicon steel cores. Smaller transformers used in electronics and consumer products are slightly less ideal, largely because of economy in use of copper and the proportionately greater leakage flux. It is difficult to measure the efficiency of a transformer directly (by comparing output with input), so the copper and core losses are usually measured or estimated instead. Core losses are usually only about 1/3 of the total.

Transformer Design

Transformer design is a well-developed subject, and the reader is referred to the many textbooks that treat it. It is important not simply to design a transformer that will do, but one that is economical, efficient and makes the best use of available materials. However, it is not difficult to design a serviceable transformer, and by understanding how this is done we will know better why transformers are as they are. As in all design processes, there are numerous trade-offs between competing requirements, and some sort of optimum is sought. On the other hand, the properties of available materials rigidly limit the possibilities.

The size, shape and material of the core must be chosen, and the number of turns of the primary and secondary windings. The size of the wire and the insulation determines if the windings will fit in the space available. The windings must be arranged for minimum leakage flux. The insulation determines the permissible temperature rise, and means of cooling must balance the loss of energy under load. We will treat only the core and the number of turns, the fundamental parameters, in our analysis. A complete design must, of course, include all these features.

Two basic equations are used in transformer design. The first is essentially Faraday's law, E = d?/dt x 108 V, where ? is maxwells (gauss times square centimeters). For transformers, this is written Bmax = ?2 E 108 / 2?fNAK, where E = rms voltage in a winding, N = number of turns, f = frequency (Hz), A = area of core (cm2), K = stacking factor (the proportion of A occupied by iron). A sinusoidal variation in flux is assumed, which is a reasonable assumption when the core does not saturate, but by no means exact. Bmax is generally assumed as a design parameter, as well as a value for E/N in volts per turn, and the necessary A results. A typical value for a small transformer is E/N = 0.1 V/turn.

Two basic equations are used in transformer design. The first is essentially Faraday's law, E = dΦ/dt x 10⁸ V, where Φ is maxwells (gauss times square centimeters). For transformers, this is written B_max = √2 E 10⁸ / 2πfNAK, where E = rms voltage in a winding, N = number of turns, f = frequency (Hz), A = area of core (cm²), K = stacking factor (the proportion of A occupied by iron). A sinusoidal variation in flux is assumed, which is a reasonable assumption when the core does not saturate, but by no means exact. B_max is generally assumed as a design parameter, as well as a value for E/N in volts per turn, and the necessary A results. A typical value for a small transformer is E/N = 0.1 V/turn.

The second is Ampere's law, H = 0.4πNI/l, where l is the length of the magnetic circuit. From the value of B_max, the value of H_max can be found from the magnetization curve of the core material, and this equation used to determine N, when a reasonable value of I is assumed (say, 5% of the full-load current).

Let's try to proportion a transformer for 120 V, 60 Hz supply, with a full-load current of 10 A. All the AC values we use will be effective values. The core material is to be silicon-steel laminations with a maximum operating flux density B_max = 12,000 gauss. This is comfortably less than the saturation flux density, B_sat. The first requirement is to ensure that we have sufficient ampere-turns to magnetize the core to this level with a permissible magnetizing current I₀. Let's choose the magnetizing current to be 1% of the full-load current, or 0.1 A. The exact value is not sacred; this might be thought of as an upper limit. From past experience, we should have some idea of the size of core that will be required. Here, we will assume a simple, uniform magnetic circuit for simplicity. In an actual case, a more complicated magnetic circuit would have to be considered. If l is the length of the magnetic circuit, H is 0.4πN(√2I₀)/l, and the magnetization curve for the core iron gives the H required for the chosen B_max. From this, we can find the number of turns, N, required for the primary.

We could also estimate the ampere-turns required by using an assumed permeability μ. Experience will furnish a satisfactory value. It is not taken from the magnetization curve, but from the hysteresis loop. Let's take μ = 1000. Then, N = B_maxl / 0.4π√2 μI₀. If we estimate l = 20 cm, the number of primary turns required is N = 1350. The rms voltage induced per turn is determined from Faraday's Law: √2 e = (2πf)B_maxA x 10^-8. Now, e must be 120 / 1350 = 0.126 V/turn, f is 60, and B_max = 12,000 gauss. We know everything but A, the cross-sectional area of the core. We find A = 2.8 cm².

This may, or may not, be an acceptable result. If not, we simply change our assumptions and try again. Design, after all, is an iterative process. By considering the above calculations, we can appreciate the changes that a different frequency, voltage and current rating, permeability or maximum flux density would produce. The number of secondary turns is now easily found from the volts/turn and the desired ratio. A 24 V secondary would have 24 / 0.126 = 190 turns.

The number of primary turns is determined so that the magnetizing current is limited to an acceptable value, and depends on the length of the core. The area of the core is determined by the required volts per turn, now that the total number of turns is known. These are the things that determine the size and weight of a transformer.

Toroidal ferrite or powdered iron cores are now easily available. Ferrite is a high-permeability, high-resistance material that has acceptable losses at high frequency. Powdered iron has granules insulated from each other for high resistivity (low eddy-current losses) and is good at moderate frequencies. Such cores can be used to experiment with transformer design, using a signal generator as a power source. The length, area and permeability of the core is now known at the beginning, making the above calculations somewhat easier. An oscilloscope can be used for measurements.

Powdered iron and ferrite cores have low B_sat and permeability values. A type 43 ferrite has B_sat = 2750 gauss, but a maximum permeability of 3000, and is recommended for frequencies from 10 kHz to 1 MHz. Silicon iron is much better magnetically, but cannot be used at these frequencies. The approximate dimensions of an FT-114 ferrite core (of any desired material) are OD 28 mm, ID 19 mm, thickness 7.5 mm. The magnetic dimensions are l = 74.17 mm, A = 37.49 mm², and volume 2778 mm³. Similar information is available for a wide range of cores. There are tables showing how much wire can be wound on them, and even the inductance as a function of the number of turns. Consult the ARRL Radio Amateur's Handbook, or specifications from Amidon Associates.

Transformers with air cores are used in radio work. They have no core losses, and are not limited in frequency (which is why they are used). A little calculation will show how hopeless an air-core transformer is at power frequencies. Air core transformers have large leakage fluxes, which cannot be avoided, and therefore poor regulation. Windings must be carefully designed to give the largest mutual flux possible.

There is a silver lining if you happen to burn out a small transformer--you can take the transformer apart to see what is inside, and analyze its design. I disassembled a transformer with a 24 VCT, 1 A secondary and 117 V primary. The primary had a resistance of 48.8Ω, the secondary 2.7Ω. The first step is to remove the mounting U bracket by bending back the tabs holding it in place. This leaves you with the core and windings, with the core tightly held by the plastic bobbin holding the windings. The windings on this transformer are wound one over the other, the secondary on top of the primary. Some transformers now use separate bobbins for primary and secondary, which are stacked on the core. This arrangement offers advantages in manufacture, but the leakage flux is probably greater than with windings one over the other.

The next step is to remove the core, which is done lamination by lamination. The core consists of E and I pieces, alternating so that successive I pieces do not fall one over the other. A suitable tool for the disassembly, which is not easy, is a small, sharp cold chisel driven by a light hammer. The first E lamination can be driven out by using the chisel at the edge of the bobbin. The laminations are glued together by the insulating substance, and have to be pried apart before they can be removed. After the first E lamination on each side is removed, things become a little easier.

The idea is to chisel off the I piece, then pry the E piece away so that it comes out. I discovered 37 laminations in the core (37 E, 35 I). The area of the magnetic circuit was A = 2.88 cm2, and its length l = 9.6 cm, found by measuring the laminations. The stacking factor K could not be determined accurately, so we shall assume that it is 1.00 without much error. The laminations were 0.50 mm thick, close to USS gauge #26. Use the DMM to verify that the surfaces of the laminations are not conducting. The total weight of the core was 224 g, about half a pound.
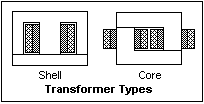
The two general configurations of iron and copper in a transformer are shown at the right. Most small power transformers are shell-type, in which the iron surrounds the copper. The ideal would be for the iron to completely surround the windings, but this is impractical. The compromise is to divide the magnetic circuit into two return paths on opposite sides of the core, as is done with the E and I laminations, as shown. Another configuration, the core type, in which the copper surrounds the iron, is common with larger high-voltage transformers, as well as with small ferrite-core toroidal transformers. Note that both primary and secondary windings are placed on each leg. The laminations are L-shaped to make a core of uniform cross-section with a central rectangular window. Core transformers are easier to insulate and to cool. If the primary winding were placed on one leg and the secondary on the other, as in the diagrams of transformers in texts, leakage flux would be excessive, and the transformer would have poor regulation (variation of voltage with load). There are other special types of construction, but all can be classified as shell or core.

Note how connections are made, and the provision for insulation. When the outside insulating material has been removed, the secondary winding can be unwound. Note the number of turns, which came out at 240 for my transformer, so that there are 10 turns per volt rms. It is now possible to estimate Bmax from Faraday's law, with the result 13 000 G, a quite reasonable result. The primary should have 1170 turns (I did not unwind the primary to find out--this would result in far too much fine wire). The magnetization curve shows that about 9.5 Oe is required to produce this flux. From Ampere's law, the primary magnetizing current should be 44 mA (rms), a reasonable figure. The primary inductance is about 7 H, from this result. The actual transformer had a measured magnetizing current of 63 mA rms. This is a relatively large value, but of little consequence in a transformer of this size.

The primary winding consisted of 0.50 mm enameled wire, about AWG #25, while the primary was 0.21 mm, about AWG #31. From the current rating of the transformer, these sizes correspond to 340 c.m./A, a somewhat adventurous figure. Note that the size of the wire has nothing to do with the magnetic design of the transformer, only with the copper loss and heating, and determines what will fit in the space provided by the core. The matter of insulation between the windings is of importance. In this small transformer, the critical point appeared to be where the primary wires were led out past the secondary winding. An extra piece of insulating cloth was used to protect the leads.

Using Transformers; Phasing

Three rules should always be observed in using transformers: first, a voltage greatly in excess of the rating should not be applied to any winding; second, a significant direct current should not be allowed to flow through any winding not designed for it; third, the frequency should not be significantly less than the design frequency. If you make the primary of a small 120 V transformer carry, say, 50 mA direct current, and then connect it to the 120 V line, you will have smoke and combustion! Applying 120 V to a 12 V secondary in hopes of getting 1200 V at the primary will have a similar result, accompanied by insulation failure which will add further fireworks. Merely overloading a transformer is not so serious--it will simply get hot and eventually burn up, or, more likely, a wire will fuse. There is normally little chance of running across a lower power frequency, such as 25 Hz. A 60 Hz transformer will draw too much magnetizing current on 25 Hz, and will run quite hot.

However, you can always apply less than the rated voltage to any winding, and use any winding as primary or secondary, so long as the current rating is not exceeded. A few milliamperes of direct current is no problem, either. Any frequency higher than the rated frequency is also safe.

Many transformers are made with duplicate windings, to permit flexibility in operation. Two 110 V primaries can be connected in parallel for 110 V, or in series for 220 V. Even more common are dual secondaries, which can be connected in series or parallel. In parallel, there will be a center tap as well. The windings cannot arbitrarily be connected to each other, because of the problem of phasing. The voltages across the windings will either be in phase, which is the desired state, or in antiphase. If connected in antiphase, the result is a short circuit.

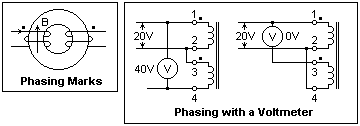
Two windings on a core are shown at the right. The black dot at one terminal or the other of each winding is called a phase or polarity mark. Currents entering the marked terminals cause magnetic flux in the same direction in the core. An increasing current entering the marked terminal as shown will cause a positive voltage at the marked terminal of the other winding. If the unmarked terminal of the winding on the left is connected to the marked terminal of the winding on the right, the two windings will be in phase and their ampere-turns will add. If they are connected in the opposite sense, their ampere-turns will cancel, and there will be no inductance. Unfortunately, transformers are not provided with phase marks, and you have to figure them out for yourself. This process is called phasing.
Of course, most transformers come with numbered terminals and wiring diagrams so that phasing is not required. Still, it is a good idea to check the phasing in any case, and to know how to do it in case you have a strange transformer without instructions. An obvious method is to use an oscilloscope and a function generator, which is easy and completely safe.

However, it is possible to phase a transformer with a voltmeter alone. I use a Variac to apply a low voltage, but a series resistance can be used to limit the current in case of an unexpected short. Apply a voltage to one of the windings, here winding 1-2. We can arbitrarily assign a phase mark to one end of this winding, say terminal 1. Connect the other end of this winding to one end of the other winding. There are only two possibilities, that we have connected to the marked or the unmarked terminal, as shown. Now measure the voltage between terminal 1 and the free terminal of the other winding (this cannot result in a short circuit because of the high resistance of the voltmeter). If you find twice the applied voltage, then conditions are as at the left. If you find zero volts, then conditions are as at the right. Now the second winding can be marked, and the proper connections determined. To phase the secondaries, measurements can be made in exactly the same way. One winding is marked arbitrarily, the other connected to its other end, and the voltage measured to the open terminal. The secondaries can be phased relative to the primary just as if they were more primary windings, provided low voltages are used and the turns ratio taken into consideration. In all these

measurements, we make use of the fact that the phase relations can be only in phase or in antiphase, which give distinctly different resultant voltages.

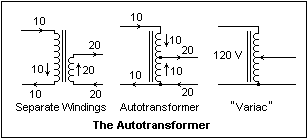
Autotransformers

In the diagram at the right, a step-down transformer is shown. The secondary voltage is half the primary, so the currents are doubled, in this example. The ampere-turns of the secondary, carrying 20 A, are opposed by the same number of ampere-turns of the whole primary. In the middle diagram, the secondary load is shown attached to the primary winding at its mid-point. Now, the ampere-turns below the connection are opposed by the ampere-turns above the connection, each excited by 10 A, but in opposite directions. The currents add at the node to give 20 A in the secondary load, as required. Conditions are just as in the case of separate windings, but without the secondary winding carrying 20 A. This is called an autotransformer, and the savings involved in its use are obvious. The disadvantage, of course, is that the primary and secondary are no longer isolated and share a metallic connection. In many applications, this is no matter, and an autotransformer can be used.

At the right is shown a "Variac" (a trade name belonging to General Radio Corporation, but now used like Kleenex and Vaseline) or variable transformer, a useful device that provides an adjustable AC voltage. For safety, the common connection must be connected to the grounded or white wire of the AC lines. If, somehow, the connection is reversed, then everything connected to the Variac becomes "hot" and hazardous. The common 120/240V converters are autotransformers, and present the same hazard.

Some early AC/DC radios (the name for those without power transformers) had only one wire in the line cord, the hot wire. The other connection was to be made to a handy pipe, which was the service ground. If the plug were inserted incorrectly, no power would be supplied, and everything would be safe. With today's polarized plugs, this is not necessary--unless an amateur electrician wired the receptacle improperly.